Eudoxus traveled and study widely - studying mathematics in Italy with the Pythagoreans, medicine and philososphy in Athens at Plato's newly founded Academy, and astronomy in Egypt. He formed his own successful school in Cyzicus, and eventually went back home to Cnidus were he was given a job in the legislature. He actually made his own observatory in Cnidus. He was a gifted mathemetician, and wrote a number of books on mathematics and astronomy. Unfortunately, none of his works survive to the this day; we know of Eudoxus based only on what other Greek writers said of him.
Eudoxus was the first person to devise a model that could explain the retrograde motion of the planets in the sky. (Keep in mind that there was not a great deal of real accurate data regarding the positions of the planets at the time.) Eudoxus was a gifted mathematician and was able to show that using three concentric spheres, one could arrange the spheres in such a way that a planet attached to one of the spheres could be made to travel around the common center, making periodic retrograde motions. Because the spheres are all concentric, this is often called the "homocentric" model of planetary motion.
So how well did the model work? Not very well, unfortunately. It had two glaring errors: the shapes of the retrograde loops in this model were always the same and it does not account the increase in brightness of the planets during retrograde motion. The success of the model, and its subsequent adoption by Aristotle, was because Eudoxus was able to create a retrograde-like motion using only spheres rotating with constant speeds. The "Principle of Uniform Circular Motion" becomes officially codified by Aristotle, but the Greeks were already preoccupied with circluar motion as a simple way to explain the seemingly complex motions in the sky. Since the model worked on a general level, if one was interested in making be exact, one need only play with the parameters (or I suppose, add some more circles.) Of course, one would need accurate data and a desire to accurately model planetary motion. I am not sure how much either of those statements applies to the early Greeks.
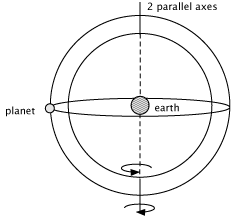Now let's try and explain what Eudoxus did. This is difficult to explain on the web (hopefully I am little clearer in class when I can try and model it.) I will build up the ideas, one sphere at a time. First, imagine that a planet is attached to a particular spot on a sphere. Earth would be at the center of the sphere, and the sphere would rotate around the Earth. As the sphere rotates, it would carry the planet around in a circle at whatever latitude we had attached the planet on to the sphere.
Next, imagine attaching that sphere to a second sphere, also centered on the earth. If the two axes are parallel, then the resulting motion of the planet with respect to the earth is simply the sum of the rotations of the two axes. If the two axes are rotating with opposite rates, then the planet would appear to be motionless, from the point of view of the earth. (This is shown in the image to the right.)
Now imagine what happens when we take the second axis of rotation and we tilt it with respect to the first. (As in the image to the left.) We will also keep the rotation rates of the two axes equal and opposite. (This is really the heart of the model.) Because the rotation rates are the same speed, but the opposite direction, the planet would almost stay in the same place; because the axes are not parallel, the planet would actually wobble a little bit left and right and also up and down. The net effect would be the planet making a figure eight loop. (The mathematical name for the resulting curve is a "hippopede.")
To make the planet actually go around the earth, and also create the retrograde motion, we take the two spheres creating the hippopede and have them rotate about a third sphere.
There is discussion over whether Eudoxus actually felt that this system was really how the planets moved or if it was just a mathematical model; no one knows. It is reasonably clear, however, that Aristotle saw the homocentric spheres of Eudoxus as real objects. (There is also some discussion as to the genesis of Eudoxus' model - the classic view is that he responded to Plato's challenge, but some are arguing that his model owes more to the Pythagoreans than to Plato.)