Born in Samos, not a lot is known about Aristarchus. Most of his work is lost, and we only know about him because other ancient Greek people talked about him.
Only one book of Aristarchus survives, "On the Sizes and Distances of the Sun and Moon." In it he proves:
While the results are off, his basic geometry and methods are sound. (Actually, the sun is about 400 times farther than the moon, and about 109 times bigger than the earth.)
Aristarchus' method for determining the relative distances to the moon and the sun is pretty easy to understand. Imagine drawing a triangle by connecting the centers of earth, moon and sun, as in the diagram below.
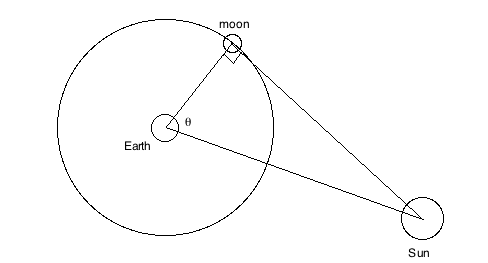
When the moon is "exactly" 1/2 full, and looks like a semicircle, then the angle earth-moon-sun is 90
, so that the distance between the earth and the sun is the hypoteneuse of the right triangle. One just has to measure the angle theta in the diagram, and we can say that the ratio of the distance to the moon to the distance to the sun is equal to the cosine of theta. Aristarchus said that the angle theta was 87, which is too small. It turns out that the angle would be just under 90. In practice, it is also difficult to accurately decide when the moon is exactly half full, and so difficult to accurately measure the angle, so while the method is correct, it turns out to be difficult to do.
Aristarchus notes that the angular size of the moon and sun are the same, which is basically true. Because of this, if the sun is about 19 times farther away than the moon, then it must be about 19 times larger.
Having calculated how much farther away the sun is than the moon, Aristarchus is then able to calculate how much bigger the sun is than the earth. To do this, he notes that during a lunar eclipse, when the moon enters the shadow of the earth, the size of the shadow is about twice the size of the moon. (Again, his data is a little off: it is closer to 3 times the size of the moon.) The image below show the moon, earth and sun during a lunar eclipse.
The image below is the one above, with some triangles highlighted.
Lastly, the image below is the triangles from above, but drawn larger and labeled.
Using the above diagram, we can make a couple approximations, and then use some geometry and algebra to find the relative sizes of the earth and sun. First, notice that the two triangles with the dotted-line bases are similar, so that we can say:
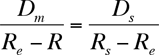
Since we know that Dm/Ds = Rm/Rs, we can rewrite the equation above as:
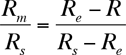
Doing a little algebra:
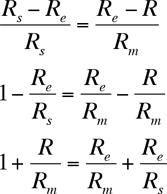
Factoring out Re/Rs from the right side:
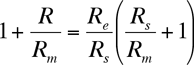
Finally rearranging we get the ratio of the radii of the sun to the earth:
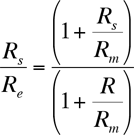
So we find that the ratio of the sun's radius to the earth's radius depends on two other ratios: the size of the sun to the moon and the size of the eclipse shadow to the moon. From earlier, Aristarchus had already found that the sun was about 19 times farther away than the moon. Because the moon and sun are the same angular size in the sky, the sun must therefor be about 19 times bigger than the moon. Aristarchus had also said that the size of earth's shadow was twice the size of the moon during a lunar eclipse. So we plug in 19 and 2 for those ratios to get:
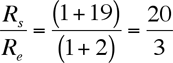
So we end up with the sun being about 7 times bigger than the earth. If we use "correct" values for those ratios, the sun is 400 times the size of the moon, and the the average eclipse shadow is about 3 times the size of the moon, which makes Rs/Re about 100; which isn't too far from the actual value of 109. In addition, since Aristarchus knew the angular size of the sun, and now the size of the sun, he can calculate how far away the sun is.
Aristarchus can then find the size and distance for the moon. Since the moon will also be 19 times smaller and closer than the sun, we know that the moon is therefor about 7/19 times the size of the earth, or about 1/3 the size of the the earth. (The correct value is about 1/4.) 
And lastly, knowing the angular size of the moon and the actual size of the moon, we can calculate the actual distance to the moon. Using the actual angular size of 1/2, and calling "R" the radius of the moon and "D" the distance to the moon, we can use a little trig to see that the moon is almost 240 moon radii away, which means that it is almost 60 earth radii away.
It should be noted that Aristarchus didn't use degrees or trigonometry as neither had been invented yet. His basic geometry and methods are valid, but for some reason his claims on some of the measurements are way off. Archimedes also states that Aristarchus had actually measured the angular sizes of the sun and moon to be 1/2, which is correct. Historians tend to think Aristarchus wrote "On the Sizes and Distances of the Sun and Moon" early on in his career, before he made more accurate measurements.
Aristarchus is also the first person to propose a heliocentric theory, though none of the actual details survive. In "The Sand Reckoner," Archimedes says:
...Aristarchus brought out a book consisting of a certain hypotheses, wherein it appears, as a consequence of the assumptions made, that the universe is many times greater than 'universe' just mentioned. His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun in the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of the fixed stars, situated about the same center as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the center of the sphere bears to its surface. (Heath, p 3)
He is basically saying that the universe is a lot bigger than everyone else is proposing at the time, and that the stars are infinitely (or at least immeasurably) far away. This way there wouldn't be any measurable stellar parallax. No one really buys into his theory, though.