Johannes Kepler was born 7 months after his parents were married. Kepler himself said he was premature, and that is why he was so sickly as a child, but there was certainly a lot of suspicion in town over what really happened. His parents didn't really get along. His father, Heinrich, had no real skills and was a mercenary, disappearing for long stretches. At one point, when he had been gone for a long stretch of time, Kepler's mother actually left him with his paternal grandparents while she went off to find him. (Somehow, she did find him and drag him back home.) Kepler's father finally left for good when Kepler was 16. While his parents were not rich, they were not poor either, and Kepler was able to go to school. He was born in Weil der Stadt, which was in the Duchy of Wurttemberg, a Lutheran stronghold in the Holy Roman Empire. (Wurttemberg is now a state in southern Germany.) His family moved a few times in the Duchy while he was a boy.
As a young boy, Kepler was very sickly. He almost died from smallpox, and suffered from the physical effects of that illness for years. He was never really fit enough to be of much use on the farm, but he quickly showed his intelligence in school. When he was 11, his early teachers picked him to take a "standardized" exam, the Landesexamen that was given to promising students. He did very well, and became a scholarship student. Because of this, he was able to continue his education in various Lutheran schools and eventually attended Tubingen University from 1588 to 1594. The Duke of Wurttemberg paid for all his education and needs, in exchange for an oath to serve the Duke until the Duke decided that he was released from this debt.
Kepler went to school hoping to become a pastor. He was deeply religious, and firmly believed in his Lutheranism. However, he got into many theological debates in which it was clear that Kepler did not blindly follow the entrenching Lutheran orthodoxy. (This caused him no end of trouble in later years.)
While in Tubingen, it also became apparent that he was a gifted mathematician, and he fell in love with the Copernican theory after one of his professors, Michael Mastlin, exposed him to it. Kepler got into many debates defending the Copernican theory. (Kepler generally liked a good debate.) The faculty at Tubingen was very conservative, both in their Lutheranism and in their astronomy. Despite his obvious talents, the faculty at Tubingen had growing reservations about Kepler. "Some of the professors had already begun to wonder if Kepler was suited for the ministry and whether he might be happier doing something else." (Connor, page 67.) When Kepler was nearing the end of his studies, there was a sudden request for a mathematics teacher in the Lutheran high school in Graz, Austria, Kepler was asked to go. Reluctantly, Kepler accepted the position, and moved to Graz. The faculty at Tubingen thought they had taken care of their Kepler problem.
While in Graz, Kepler publishes his first book, Mysterium Cosmographicum in 1596 and gets married to Barbara Muller in April 1597. In February 1598, the Keplers have a boy, but little Heinrich dies when he is only two months old. They very quickly have a little girl, Susanna, and she also dies at only one month old. During this time, in September of 1598, the Archduke Ferdinand (an heir to the Hapsburg Empire of which Austria was part) gave an order to close down all the Lutheran schools and churches in Graz and Judenburg, and all the ministers and faculty were exiled from the lands of the Archduke. Kepler is forced to leave Graz, leaving his wife behind. After only one month, Kepler gets special permission to return to Graz - and is appointed the district mathematician.
Kepler had been in correspondance with Tycho Brahe who happens to become the Imperial Mathematician for Empororer Rudolph II in Prague in 1598. (Rudolph was Ferdinand's uncle.) Brahe invites Kepler to come visit him, which eventually turns into an offer to work for Brahe in 1600. Conveniently (for astronomy's sake), all the Lutherans are finally kicked out of Graz in 1600, so he really doesn't have a choice.
Brahe and Kepler have a very stormy relationship - each needing the other to prove their own ideas were correct. Brahe needs Kepler's mathematical abilities to prove his model of the solar system was the correct one and Kepler needs Brahe's data to prove his ideas from the Mysterium Cosmographicum. It was during this time that Kepler began working on the problems with the orbit of the Mars. While Brahe got Kepler working on Mars, he did not give Kepler the data that he needed - and the two often got into arguments. When Brahe dies in 1601, Kepler is quickly appointed the new Imperial Mathematician and he finally gets access to all of Brahe's data.
Kepler stays in Prague until 1612. During that time, he publishes a number of books, the most notable being Astronomia Nova, but also a book on optics. Rudolph II loses power, and then dies, in 1611 when his brother Matthias pushes him out the door. Matthias is not as open-minded regarding religion as Rudolph II was, and
Being the only "public" Lutheran took a toll on Kepler. While his fame kept him safe from the Counter-Reformation, his friends and acquaintances began to distance themselves from him for fear of being caught up in the religous turmoil.
(Bio still needs to be finished.)
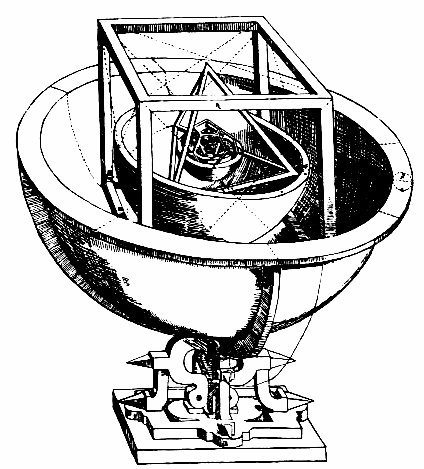
From his days as a student, Kepler was a Copernican.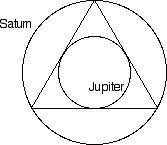 
Starting in 1591, Kepler was an astronomy and mathematics teacher in the Lutheran school in Graz. One day he was in the middle of a lecture concerning the orbits of Jupiter and Saturn when he noticed an interesting geometrical fact: one could draw an equilateral triangle whose vertices all (nearly) hit the orbit of Saturn and at the same time, the orbit of Jupiter was tangent to the sides of the triangles. (See diagram at right.) Kepler was struck by the idea because he thought it may be a clue as to why the planets were spaced the way they were. (Remember: in the Copernican system, the planetary orbital sizes have fixed ratios, unlike the Ptolemeic system where all the planetary orbits are independent of each other.) He finally published his idea in 1596 in a little book called Mysterium Cosmographicum. Kepler proposed a geometric system involving 6 nested spheres and one of each of the 5 Platonic Solids. Each sphere was the radius of a planetary orbit. Each Platonic solid had a sphere inscribed into it, tangent to its faces, and a sphere hitting all the vertices. There were only 6 planets orbiting the sun because there were only 5 Platonic solids to act as spacers for the orbits. Kepler also proposes that the planets are all moving around the sun due to a force somehow exerted by the sun on the planets, and that this force weakened the farther from the sun a planet was. The diagram below represents the solar system according to this scheme.
For help in getting his book published, he wrote to Maestlin, his old professor. Maestlin was generally impressed with Kepler's book, but he had concerns with Kepler's idea that the sun was somehow driving the solar system. Mastlin "worried that this blurred the line between astronomy and physics. Traditionally, astronomy was about geometry, but about creating hypotheses that accounted for the appearances for what people saw in the sky, while physics was about explaining movement on earth or in the atmosphere just above the earth, in the world under the moon." (Connor, page 94.) Ironically, the thing that worried Mastlin the most was the the only concept that proved correct in the whole book. Mastlin's worries were in fact echoed by many astronomers; they were intrigued by Kepler's math, but disagreed with his physics.
Mysterium Cosmographicum was Kepler's first book, and also the first published defense of the Copernican system. It readily established himself as a very capable mathematical astronomer, and Kepler became somewhat of a celebrity. (This was why he was allowed back in Graz after the Duke kicked out all the Lutherans.) As was custom, Kepler sent numerous copies of the book to influential people, including Tycho Brahe. After a couple years of correspondance, Brahe is kicked out of Denmark and ends up in Prague as the Imperial Mathematician to Emporer Rudolph II. Right after this, Kepler is forced out of Graz for good when he refuses to become Catholic. As a result, Kepler moves up to Prague and ends up working with Brahe in the begining of 1600.
Brahe and Kepler do not get along. Their personalities are completely opposite and they are working for different things. Brahe needs Kepler's mathematical ability to prove his model is correct, while Kepler needs Brahe's data to improve his ideas from the Mysterium Cosmographicum. Brahe gets Kepler to work on the problem of Mars' orbit. Of all the planets, calculating the position was the most difficult and Brahe and his assistants had not been able to figure it out. (In reality, it is because Mars has the least circular orbit of the then known planets.) However, Brahe won't give Kepler complete access to the data he needs. They fight,they make up, they fight, they make up and who knows how long this would have gone on when Brahe suddenly dies in 1601.
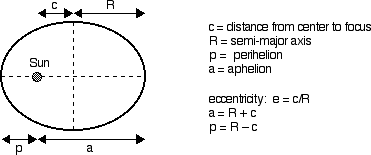
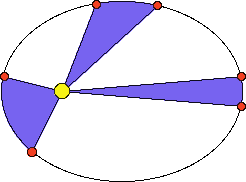
After Brahe's death, Kepler is quickly appointed the Imperial Mathematician and given access to all of Brahe's data. (There was a struggle over control of the data with Brahe's family, but Kepler ends up with the data, but the family ends up with some editorial control over any book that Kepler publishes using the data.) Kepler finally has all the data he needs to solve the problems with the orbit of Mars. It took Kepler years to figure out the shape of the orbit, and his efforts mark a turning point in doing mathematical science and are still a modern day example of how a good scientist works. Kepler, like all mathematical astronomers of his day, began by trying circular shapes for the orbit, but he could never get it to work. Kepler came up with a number of ways of dealing with multiple data sets, and was actively concerned with how much error was in the data and how accurate the data really was. At one point, he thought he had found a solution, but when he went to check his idea with some different data, he found that his predictions differed from Brahe's data by 8 minutes of arc. This was an order of magnitude better than any other planetary model in history, but he knew that Brahe's data was off by no more than 2 minutes of arc. Kepler reluctantly went on with his calculations, trying new orbital shapes. Finally, during Easter of 1605 he solves the problem and realizes that the orbit of Mars is an ellipse, with the sun at one focus. Prior to this, he had discovered his equal area law, which described how the speed of Mars changed as it went around the sun. A few years later, in 1609, he is able to publish Astronomia Nova, or The New Astronomy, in which he details his struggles with the planet Mars and gives his results.
It should be stressed that Astronomia Nova was truly a New Astronomy. While Copernicus had made the earth just another planet, in many ways the Copernican model was a return to a more perfect Aristotelian cosmology because the Copernican model more closely followed the Principle of Uniform Circular Motion. Copernicus was not interested in the causes of the motions, he was interested in describing the motions using circles. Kepler not only discovers the actual orbital shapes of the planets and throws out the circles, he throws out Aristotle completely by arguing for the causes of the orbits in the sun. Kepler is pushing astronomy into reality, insisiting that the earth really is moving and the sun is not only at the focus of the orbit, but actually causes the motion of the planets. This is a huge break from the way astronomy was done and thought about; astronomers didn't really care about what the planets really did, they only wanted a pretty theory using perfect circles that could predict where to find a planet.
I think the following quote from the introduction to Astronomia Nova captures the essence of Kepler:
Advice for Idiots.
But whoever is too stupid to understand astronomical science, or too weak to believe Copernicus without affecting his faith, I would advise him that, having dismissed astronomical studies and having damned whatever philosophical opinions he pleases, he mind his own business and betake himself home to scratch in his own dirt patch, abandoning this wandering about the world.(Donohue, p. 24)
By 1618, he had discovered a third law, called his Harmonic Law, in which he discovered the relationship between the period of a planet around the sun and its distance to the sun. These results he published in Harmonice Mundi, or Harmonies of the World. He went to great lengths to try and talk about celestial harmonies - literally looking at various planetary ratios and relating them to musical harmonies.
 |  |  |  |  |
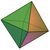| tetrahedron | octahedron | icosahedron | hexahedron | dodecahedron |
The images above are from http://en.wikipedia.org/wiki/Platonic_solid, which also has a nice description of the solids with a lot more of the math behind them.