Concepts
Miscellaneous
compared to the plane of the earth's orbit around the sun, as shown in the diagram below:
As the earth travels around the sun over the course of a year, it spins on its axis with a constant angular velocity. Because there is basically no external torque on the earth, this velocity is constant in both magnitude and direction. This is a long-winded way of saying that the axis of the earth's rotation points to the same spot on the celestial sphere as it goes around the sun. This spot is very close to the North Star.
The earth's rotation axis is tilted by 23.5 compared to the plane of the earth's orbit around the sun, as shown in the diagram below:
Because the rotation axis is tilted to the orbital plane, we have seasons. When the northern hemisphere is pointed "towards" the sun (A), it is summer in the northern hemisphere and therefor winter in the southern hemisphere. Likewise, when the northern hemisphere is pointed "away" from the sun (C), it is winter in the northern hemisphere (and summer in the southern.) In the spring and fall, neither hemisphere is pointed towards or away from the sun (B and D).
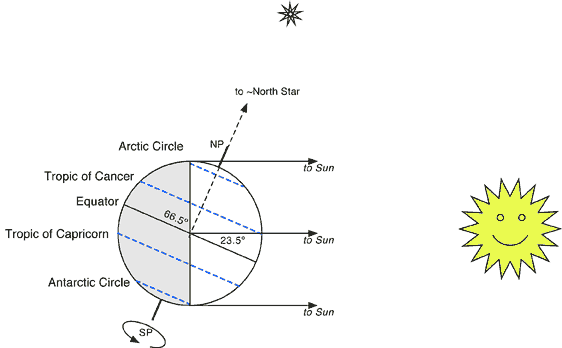
The diagram above would represent the earth and sun on the summer solstice for the northern hemisphere. We are assuming that the sun is pretty far away (which it is) so that no matter where you are, the sight lines to the earth would all be parallel. Three of those lines are shown in the diagram. Reality is that they do converge very slightly, but it is really hard to measure this, and is called the parallax of the sun. Also notice the left half is shaded, because that half of the earth would be experiencing night time and not see the sun.
On the summer solstice, a line drawn from the center of the earth to the sun would pass through the latitude known as the Tropic of Cancer, which is about 23.5. That means on the summer solstice, the sun would be directly overhead at noon if you were on that latitude. Any location north of this latitude, the sun will never be directly overhead at any point in time. For all the locations in the northern hemisphere, there is more daylight than night and the sun gets very high in the sky at local noon.
If you were on the latitude 66.5 (the Arctic Circle) on the summer solstice, something very different would happen. Notice that any sight line from the Arctic Circle to the sun would be in daylight. There is one sight line where the sun would just be onthe horizon (that is the top line in the diagram above). So the sun would never actually set! "Sunset" would happen at local midnight, and the sun would only hit the horizon and then rise again. At latitudes below the Tropic of Cancer, the sun will always be below the horizon every single night, while above it, there will be periods of time where the sun never sets. At the North Pole, the sun hasn't set for months, and it will be months before it does set
The opposite is going on in the southern hemisphere. There is more night than day and at noon, the sun doesn't get very high in the sky. Between the South Pole and the Antarctic Circle, the sun won't rise at all on this day. At the South Pole, the sun hasn't been seen for months, and it will be months before it is seen.
This isn't related to the solstice, but also notice that the axis of the earth's rotation points to (basically) the North Star. No matter where you are on the earth, the sightline to the North Star would be parallel to the dotted line from the middle of the earth up through the North Pole.
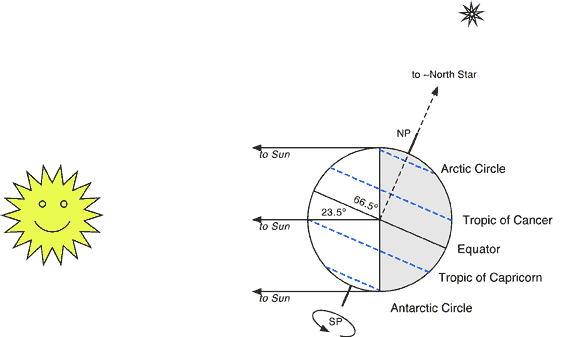
6 months later, the earth is on the other side of the sun, but its axis of rotation is still pointing to the North Star. This causes the northern hemisphere to point away from the sun and the southern hemispher to point towards the sun. In the northern hemisphere, this would be the Winter Solstice, as it would be when the sun is at its lowest maximum height of the year and the day is the shortest of the year. (So the southern hemisphere would call this their Summer Solstice, and it would be their longest day of the year.)
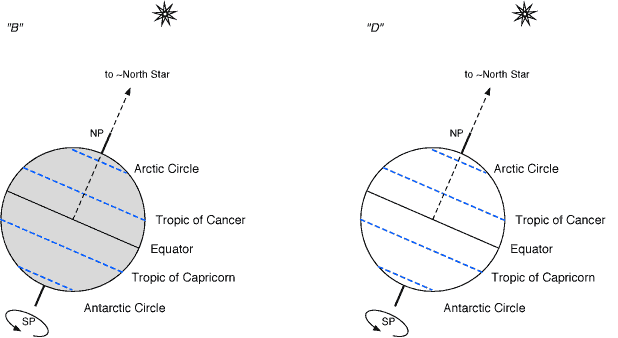
The two images above are an attempt to show the situation on the equinoxes, keeping the tilt of the earth oriented the same way. The picture on the left would be as in position "B" from the very top of the page. This means that the sun would be behind the earth in this picture, so we are looking completely at the night side of the earth. Notice that we are centered on the equator, and we can just see both poles.
The picture on the right represents position "D", so in a sense we are sun shining down on the earth. Again, notice how we are centered on the equator and how we can just see both poles.
On the equinoxes, the sun would be directly over the equator. At either pole, the sun would be just on the horizon. If the earth didn't move (and if there was no atmosphere) then we could say that day and night were of equal length all over the earth. On the equator, the sun would rise exactly in the east, go straight overhead and set exactly west. On both poles, the sun would be right on the horizon and simply rotate around the entire horizon. (The fact that the earth also moves around the sun breaks some of the symmetry, and atmospheric effects add to some more, but hoepfully you get the basic idea.)
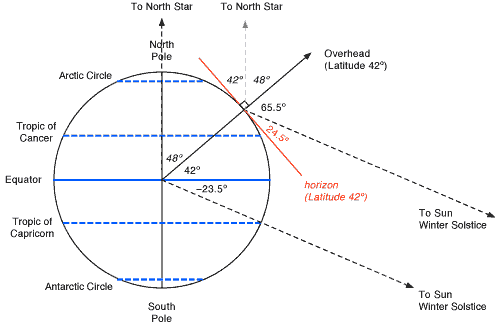
There is a lot going on in the diagram above, but notice it is rotated compared to the two previous diagrams. It shows how to find the North Star for a particular latitude. More importantly, it shows an example of how to find the maximum height of the sun for a particular latitude on a particular date (the Winter Solstice in this case.)
In either case, you have to find your location on the earth, figure out what overhead and the horizon mean. In this example, we are using a latitude of 42
North. By definition, we draw a line up 42 from the equator (or 48 down from the North Pole). Then we can draw a line from the center of the earth up through this point. This would then point in the direction of directly overhead at that latitude. By definition, the horizon is perpendicular to this, and is shown in red in the diagram above.
The easy one is the position of the North Star. A line from the center of the earth through the North Pole basically points to the North Star. (It is off by almost 1 degree actually, but I will ignore that in class.) Then draw a line parallel to this from your location on the earth (which we found above); this will also point to the North Star. These are the vertical dashed lines in the diagram above. Because the dashed lines are parallel, the angles are as shown. The end result is that the angular height of the North Star is your latitude.
To find the maximum height of the sun, you have to first figure out where the sun is. Draw a line from the center of the earth through one of the tropics or the equator, depending on the date. (All I will ask you is on the equinoxes or the solstices, so you don't have to worry about how the location of the sun varies with time on other days. Google it if you care.) In this case, we said the Winter Solstice, so the line goes through the Tropic of Capricorn. Then draw a second line parallel to this but starting from your location on the earth. These are the two diagonal dashed lines in the diagram above, and these are the directions to the sun. Once again, we have parallel lines, so we can figure out the angles. In this particular case, the sun would be 65.5 from overhead or 24.5 up from the horizon.