Historical Astronomy: Concepts: Models of the Solar System

In class, we discussed three main models of the solar system that were used to calculate the positions of the planets and stars: the ancient Greek geocentric model as proposed by Ptolemy, the full heliocentric model by Copernicus, and the hybrid of these proposed by Brahe. Despite their philosophical differences, all these models were mathematically the same. They all relied on combinations of circles moving at constant speeds in order to work. The only real mathematical difference between them is the choice of origin and coordinate system. They were all wrong. (Kepler finally figured out that the planets traveled in ellipses around the sun in the begining of the seventeenth century.) Below are summaries of the three models, along with the "pros" and "cons" of each, as debated in the sixteenth century. Follow the links to the individuals for more details of each person and what they did.

Ptolemy

Ptolemy produced the first fully working model of the solar system in the second century AD, and his work was the foundation for mathematical astronomy until the end of the sixteenth century. This model was based on the ancient Greek "Principle of Uniform Circular Motion," which stated that the only motion that could last indefinitely was heavenly motion in a circle at constant speed. It was also completely geocentric; the earth was in the middle of the universe and did not move.

There were two main circles that carried each of the planets. The mechanics for each planet is shown in the diagram below:

Each planet, M, traveled in a little circle called an epicycle. The epicycle rotated about its center, P, at a constant rate. The center of the epicycle traveled in a larger circle called the deferent. The center of the deferent, C, was not exactly on the earth, E, but close to the earth. The point labeled Q was called the equant point, and EC = CQ. We have two circles and those circles had to rotate at constant speed. In the Ptolemeic model, the epicycle did rotate with a constant speed, so that PM rotated at a constant rate. However, the center of the epicycle itself did something a little weird. Ptolemy had the line QP rotate at constant speed. This meant that the planet actually traveled around the deferent at different speeds. (Reality is that the planets speed up when they are closer to the sun, and slow down when they are farther.) The equant was Ptolemy's big invention, and while it made the model more accurate, it also annoyed the purists who believed in the Principle of Uniform Circular Motion.

The epicycle was needed in this model to get the position of the planet correct, and to explain retrograde motion. If the epicycle rotation was faster than the deferent rotation, then the planet would actually go backwards when the planet was closer to the earth.

The diagram below shows the ordering of the planets in the Ptolemeic model.

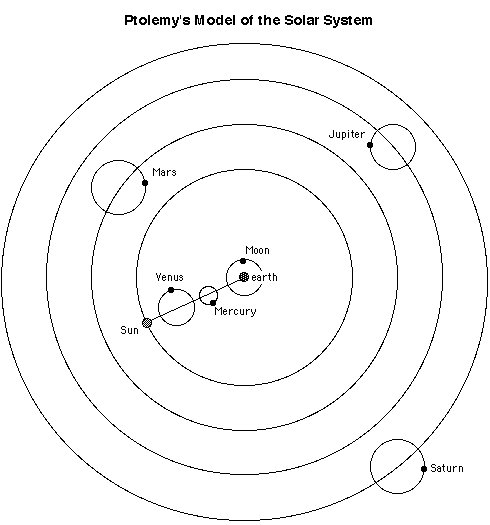
Note that the order is correct, if we just switch the earth and the sun. Also, each planets parameters (distances and rotation rates) were all independent of each other. One could adjust the size of one planets orbits, and it would have no effect on another planets. Also, though I didn't show it, the sun and moon were also on epicycles. I also did not show the deferents for Venus and Mercury, but their centers were tied to the rotation of the sun around the earth.

There is a great shockwave file which I got from http://astro.unl.edu/naap/ssm/ssm.html. You can play with parameters to see what happens to the resulting orbits. It is definitely worth the look.

Copernicus

In 1543, Copernicus published "On the Revolutions of the Heavenly Spheres." This was the first new fully worked out idea in mathematical astronomy since Ptolemy 1400 years earlier. He proposes that the earth is just another planet, and that the sun is at the center (actually close to the center) of the solar system. Copernicus believed very strongly in the Principle of Uniform Circular Motion; so he still had to use epicycles to predict the planets' positions. Unlike Ptolemy, however, epicycles were not needed to explain retrograde motion. Copernicus, correctly, states that planets don't actually go backwards, they only appear to go backwards because the earth is also traveling around the sun. When the earth is either lapping an outer planet, or being lapped by an inner planet, the other planet would appear to be going backwards from the earth's point of view. Because the earth was just another planet, if the distance for one planet changes, all the distances have to change. Copernicus does have the order of the planets correct, and also calculates their sidereal periods correctly. In addition, the rough size of each orbit is pretty close to the true average distance to the sun. Each planet, however, has its own center of motion, all of which are pretty close to the sun. The sun just happens to be close to the center of everything in this model, and doesn't actually do anything.

As above with Ptolemy, there is a great shockwave file which I got from http://astro.unl.edu/naap/ssm/ssm.html that lets you play with various parameters and see how the model works. This may be especially useful to see how retrograde motion actually happens. (To see the retrograde motion, look at the "Zodiac Strip" in the bottom left and watch how the planet moves along the zodiac, as seen from the earth.)

Brahe

In the end of the sixteenth century, Brahe proposes his own hybrid model of the solar system. (I do not know how much mathematical detail he ever published, though.) Brahe liked the Copernican model except for thing: he didn't think the earth could be moving without it being obvious to people on the earth. (Like many people, he really did not understant inertia.) He felt that the earth had to be at rest. In his model, the earth is at rest, and the sun travels around the earth. However, all the other planets travel around the sun. (This actually gets messy with the orbits of Mars and the earth intersecting.) The diagram below shows the orbits. Because Brahe used circles, he also used epicycles, which I did not put in the diagram.

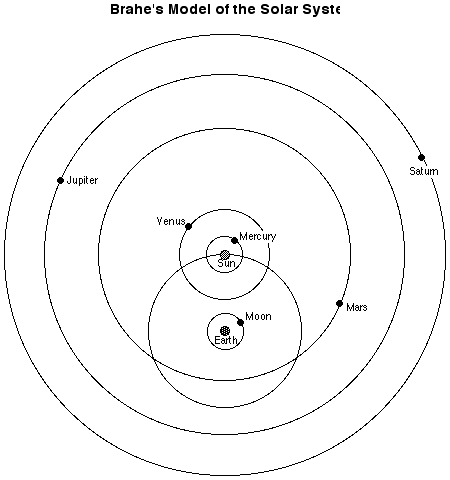
last updated 3/5/08 by david mcclung, copyright 2008. All rights reserved.