| Home | Ancient Greeks | Scientific Revolution | Observations | Concepts | Miscellaneous |
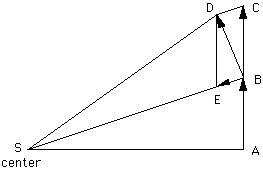
After stating his 3 Laws of Motion, the first thing Newton proceeded to show was that for any central force, the area swept out per time will be a constant. (A central force is a force that is always pointed to a center, as the force of gravity on the earth is always pointed to the sun.) He used a geometrical argument similar to the following:

Imagine that a body has a certain velocity, and so would have traveled the vector AB in a certain amount of time. If there were no forces on the body, in the next amount of time, it would have traveled the vector BC. If there were a central force acting on the body, then the force would have acted towards the center shown, and the forced would have changed the velocity of the body by the vector BE. To find the resultant vector, we simply add the change in velocity to the original velocity, using the parallelogram BEDC, to get the resultant vector BD. (We could then say there would be another change in velocity, pointed along the vector DS, but of some other length, and draw a similar set of parallelograms to get the body going around the center.)
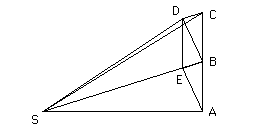
Draw in a couple more segments, SC, and EA. It can be shown that the areas of the following triangles are all equal: SBD = SBC = SBA. Since the areas were all created in the same amount of time, then the area swept out will be the same for the same amount of time. Note that it does not matter how the force varies with the distance, all that matters is that the force always be directed to the center.
To show the areas are the same:
triangle SBC = triangle SBD because they are two triangles with the same base (SB) and the same height (BD because EBCD is a parallelogram, DC is parallel to SB.)
triangle SBD = triangle SBA because they are also two triangles with the same base (SB) and the same height. triangle BCD is congruent to triangle EBA: angle DCB = angle EBA because DC is parallel to EB and ABC is a line. DC = EB because EBCD is a parallelogram. CB = AB because if there was no force, the velocity would not have changed. By Side-Angle-Side, the triangles are congruent, so therefore they have the same height. The heights of the little triangles are the same as the heights of the larger triangles (height of triangle EBA is the same as the height of triangle SBA and the height of triangle ABD is the same as the height of triangle triangle SBD.)
Forces do not turn on and off, but act continuously. If we imagine that the chunks of time we are considering are infinitely small, then the above diagrams become "correct."
Note that another common derivation is based on the conservation of angular momentum.
For a central force acting on a body in orbit, there will be no net torque on the body, as the force will be parallel to the radius. Since the net torque is zero, the body will have a constant angular momentum. Therefore:
where r is the radius of the orbit, m is the mass of the body, and v is the velocity. (for this we will assume the simple case of a circular orbit, but for non-circular, all we need to use is the tangential velocity in the following.)
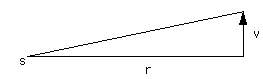
The area A swept out in a time t will be A = (1/2)r(vt). (For infinitely small time t, this true.)
Combining these two equations, we can say
L/2m is a constant, since the mass and angular momentum are constant, so that area per time is a constant. The planet would sweep out equal areas in equal times.