To measure the distance to a distant object it is easy to use triangulation. Triangulation is based on the idea of parallax, or the apparant change in position of a stationary object due to the change in position of the observer.
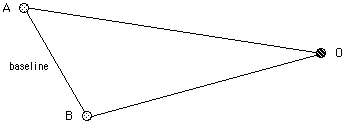Generically, to measure the distance to an object, O, you need to look at the object from two different places, A and B. The distance between these places is called the baseline. By measuring the distance of the baesline, and the two angles OAB and OBA it is easy to use trigonometry to calculate the position of the object. (Law of Sines would be very useful for the diagram shown.)
Astronomically, stars are so far away that it is impossible to measure any parallax for any stars by looking from two different positions on the earth; they are just too far away. However, by making observations 6 months apart, it is possible to measure parallax because the baseline is then the diameter of the earth's orbit around the sun. Even then, it is difficult to do, and it wasn't until 1838 that stellar parallax was first measured.
The diagram above shows the situation for stellar parallax. The angle 
is called the parallax angle. The distance d is the distance from the sun to the star. (When measuring distances to stars, the standard is to measure from the sun, since the earth is moving around the sun.) It should be obvious that we can say:
= 1/dThis will give us "d" in astronomical units (AU.)
For more information, here are some links:
http://www.astronomynotes.com/starprop/s2.htm