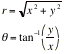In class, we use Cartesian coordinates for all our work. Most of the time, this is the easiest coordinate system to use. It is important to realize that the choice of a coordinate system should make the problem easier to use. We see this when we do problems involving inclined planes, where it is easier to use a coordinate system that is “parallel” and “perpendicular” to the inclined plane. Sometimes it very useful to use polar coordinates instead of Cartesian; especially when the problem involves quantities that change only with the radius.

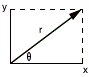
The point (x,y) would be given in polar coordinates by the pair (r, q), as shown. It should be obvious from the diagram that we have the following relationships between the coordinates:

Cartesian to Polar	Polar to Cartesian

Position Vectors

The fun begins when we wish to describe position vectors. In Cartesian coordinates, we would describe the position of an object at (x,y) with the vector

A unique aspect of Cartesian coordinates is that the unit vectors i and j always point in the same direction and are independent of each other. In polar coordinates, however, the two unit vectors, r and q, do depend on each other, and change their direction.

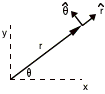
The unit vector in the radial direction is labeled , and the unit vector perpendicular to that is labeled . The radial unit vector always points away from the origin, so it actually points to different directions depending on the value of q. The angular unit vector always points perpendicular to the radial unit vector. We could relate the polar unit vectors to the Cartesian coordinate vectors with the following:

That means to write the position of an object in polar vector notation, we would simply write

This looks odd, but remember that the unit radial vector depends on q, and is not constant.

Velocity Vector in Polar Coordinates

The velocity of an object is found in Cartesian coordinates by

In polar coordinates, the velocity vector is given by

Remember that both the radius and the unit radial vector can change, hence the more complicated derivative than the Cartesian velocity.

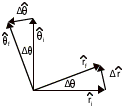
So how does the unit radial vector change in time? To see this, the following diagram represents an initial and a final unit radial vector, and the change between is labeled ∆r.

In the limit as delta-time becomes zero, we can say that . The magnitude of is 1 (by definition) and the direction of is in the direction of . Looking at the magnitudes, we have

so that ,

which in the limit becomes

Combining this with the direction, we have

Likewise, we can do the same thing to find an expression for . The magnitude is the same, but the direction is opposite the unit radial vector, so that we have

We can substitute the first expression in to get the following expression for velocity in polar coordinates

The first term in the velocity is the radial velocity and the second term is the tangential velocity (which is often written as rw)

Acceleration Vector in Polar Coordinates

To find the expression for acceleration, we take the time derivative of the velocity, as follows

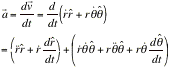
Substituting the expressions for the time derivatives of the unit vectors

So that we get the following expression for acceleration

The first two terms are the radial acceleration terms: the linear acceleration and the centripetal acceleration. The second two terms are the tangential acceleration terms: the linear tangential acceleration and the more obscure Coriolis acceleration.

Example

1. Suppose we have an object that travels in a circle of constant radius 3 meters with a constant angular velocity of 2 radians per second. What are the expressions for the position, velocity and acceleration as functions of time?

a. The position as a function of time is trivial: r(t) = 3 and q(t) = 2t.

In Cartesian coordinates, the position would be given by x(t) = 3cos(2t) and y(t) = 3sin(2t).

b. The velocity would be given by , so that

.

The velocity would have a radial speed of 0 m/s and a tangential speed of 6 m/s, both of which were constant; i.e. the object would be traveling in a circle with a constant speed of 6 m/s.

In Cartesian coordinates, the velocity would be

.

c. The acceleration would be given by , so that

which is simply

The acceleration has a constant magnitude of 12 m/s² and is directed to the origin. (Remember that positive points away from the origin.) This is the centripetal acceleration! Recall that a_c= v²/r, so that a_c = (6)²/3 = 12. There is no tangential component of the acceleration.

In Cartesian coordinates, the acceleration would be