(adapted from Fowles “Analytical Mechanics, 3^rd Ed.”, 1977)

In polar coordinates, Newton’s Second Law for an object of mass m is

For a central force, the second term is zero. (By definition, a central force depends only on the distance from the origin, and is independent of angular position.) Calling the central force function f(r), we can break up the above into two equations:

1.

2.

In principal, given the force function, one can then solve the differential equations to find r and q as functions of time. Since we want to find the shape of the orbit, we need to find r as a function of q. To do this, we will change variables, letting r = 1/u.

The second equation implies that is a constant; which means that the angular momentum is constant. To see this,

So the time derivative of is zero, which means that it is constant. If we call L the angular momentum, we can define the constant h to be

To change the variables, we need to find expressions for all the variables in equation 1.

By definition, we have

i.

From the constant h above we have

ii.

We need to differentiate equation i twice to find an expression for , so

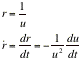
This can be rewritten as

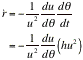
So that we get

Differentiating a second time gives

Doing several steps in a row:

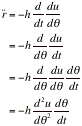
Substituting equation ii we get

So that we have

iii.

Substituting these three equations into equation 1 we get

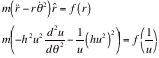
We finally have our generic differential equation for the orbit:

3.

Equation 3 is the general differential equation of the orbit for any central force. If the central force is Newton’s Law of Gravitation, then we have the following for f(r) and thus f(1/u):

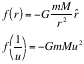
Note that the minus sign is because the unit radial vector points away from the center, and the gravitational force pulls the planet into the center. Also note that M represents the mass of the sun, and m the mass of the planet.

Substituting this into our equation of the orbit (3) we get

This is a relatively simple differential equation with the following as a solution

(To see that this is the solution, apply it to equation 3.) The term A is a constant of the integration, and depends on the orbital conditions of the planet. The term is a constant of the integration, and is simply the initial orientation of the orbit. To keep things simple, lets call it 0. Changing our units back to the original gives us the following as the equation of the orbit for any body under the influence of gravity:

This is the equation for a conic section in polar coordinates! We can rewrite it in the more standard form

with the eccentricity

A is then the inverse of the distance between the focus and the directrix. Putting the equation in terms of the closest distance between the sun and the planet (the perihelion distance) r₀ gives us the following:

with and

For an inverse-square central force, the resulting orbit will be a conic section; the actual orbit will depend on the eccentricity as follows:

eccentricity	resulting orbit
e = 0	circle
e < 1	ellipse
e = 1	parabola
e > 1	hyperbola