Conic sections are the family of curves that result from the intersection of a plane with a cone. Depending on the angle at which the plane intersects the cone, the resulting curve will be an circle, ellipse, parabola or a hyperbola.

It turns out that the general definition of a conic section depends on the distance between a fixed point, called the focus, and a fixed line, called the directrix. In the diagram below, the focus is labeled F and the directrix is labeled D.

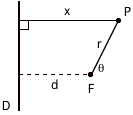
A curve that is a conic section will be defined as the set of all points, P, such that the distance to the focus, r, and the distance to the directrix, x, is

r = ex

where the constant e is called the eccentricity. It turns out that if e < 1 then the curve is an ellipse. If e = 1, the curve is a parabola. If e > 1, then the curve is a hyperbola. (A circle is the special case of an ellipse, where e = 0.)

Applying this definition to polar coordinates, with the origin at the focus, the point P is at the position (r,q), so that

The variable d is the distance between the focus and the directrix. Solving the above for r we get

We could have done the above with the directrix to the right of the focus, the only difference is that we would have

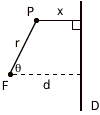
so that

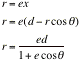
We could also look at putting the directrix above or below the focus, and we would get the same equation, except we would have sines instead of cosines. Rather than go through all the special cases, we’ll just use the above, and realize that the only difference between all the cases is really just the initial orientation.

If we call the minimum distance between the focus and the curve r₀, then we can see that this corresponds to the when the angle is either 0 or π, depending on whether the directrix is to the right or the left. We can rewrite the above equations as

r₀ when q = 0

so that we have

Substituting this in to the original equation we get

(For the case of the directrix to the left, q = π, and we end up with.)

This form of the equation is useful when talking about orbits of the planets, because the sun would be at the focus, and the distance r₀ would be the closest the planet and the sun are, called the perihelion distance.

You can look up in any math book to see how to go from this general definition to the Cartesian coordinate version, and also for examples showing the different curves based on the eccentricity.

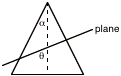
But why are these called “conic sections?” Since these proofs are not in standard math books, we’ll do them here. (This proof adapted from http://xahlee.org/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html) Let’s define a couple of angles. The diagram shows the side view of a right circular cone being intersected by a plane. The vertex of the cone is a, and the angle at which the plane intersects the axis of the cone is q. (As an aside, if q = 90º, then the intersection is a circle, if q = a, then the intersection is a parabola, if q > a, then it is an ellipse, and if q < a, then a hyperbola.)

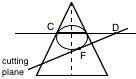
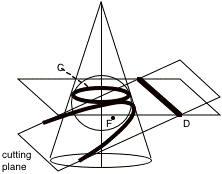
To prove that we get a conic section from the intersection, inscribe a sphere into the cone so that it is tangent to the intersecting plane (which we’ll call F) and tangent to the cone in the circle C. Then extend out the plane that contains the circle C until it also intersects the cutting plane in the line D, as in the diagram to the right. The point P will be any point on the intersection of the cutting plane with the cone; our conic section. (It turns out that the point F is the focus for the conic section and the intersection of the two planes is the directrix.)

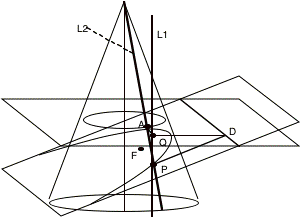
Through the point P, draw a line that is parallel to the axis of the cone. The intersection of this line and the circle plane we’ll call Q. Draw another line through the point P, except this line passes up the side of the cone to the apex of the cone. The intersection of this line and the circle C we’ll call A. Lastly, draw a line from the point Q to the point A and a line from the point P to the point F.

Because the line segments PA and PF are both tangent to the original inscribed sphere, and both pass through P, they are the same length (PF = PA.)

We also have two right triangles with a common side: PQA and PQD. ÐDPQ is q and ÐQPA is a. Therefore we can say that

Equating these we get

Since PA = PF, we can write

Since the cosine terms are constant, this is the same as our original definition of a conic section! (PF is the distance from the point to the focus, and PD is the distance from the point to the directrix.)